 |
 |
A true Normal Distribution, also known as a Gaussian distribution, would produce a "bell-curve". An example of this is ploting the number of people of a certain height in a population. The graph would form a bell-shape curve similar to that shown in the diagram below.
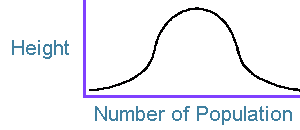
The low point at the bottom left corner indicates the small number of people of very short height. Moving to the centre of the graph the curve rises as the majority of the population is of around average height. Then the right hand tail of the graph indicates the small number of very tall people. The curve looks like a bell shape, hence the name "bell-curve". Stock and share prices do not always form an exact "Normal Distribution". A graph of price data over a period would look similar to the classic bell-curve but there would probably be some slight difference - the extreme left and right of the curves for stock prices are often slightly higher than would normally be expected. This is a phenomenon known as "fat tails". As a result, stock and share prices which are more than two multiples of the standard deviation away from the average may be slightly more common than the statistical 95.4% which would be expected for a "Normal Distribution". Similarly, prices whch are over three multiples of the standard deviation away from the average can be more common than the 99.73% predicted by normal statistical analysis. There are a number of theories regarding the possible reasons for stocks and shares not following exactly the normal bell-shaped curve of Normal Distribution. One possibility is the "Herd Mentality" of some investors. If a stock price is rising of falling considerably, investors may follow the trend and buy (or sell), thus increasing the extremity of the rise (or fall). Alternatively, a similar effect is caused by market followers who see a stock break outside of its normal trading range and buy (or sell) in the theory that the breakthrough indicates the stock may be moving permanently to a new higher (or lower) trading range.
|
| Moving Average | MFI - Money Flow Index | Exponential Moving Average |
| RSI - Relative Strength Index | Moving Average Envelopes | ROC - Rate of Change |
| Fast and Slow Stoch Stochastics | W%R - Williams' %R | MACD |
| Standard Deviation Definition and Usage | Calculation of Standard Deviation | Normal Distribution and Standard Deviation |
Plus more useful stock market and share information:
| Online stockbrokers | Stock analysis software and online services |
Please bookmark Pandacash's Normal Distribution and Standard Deviation of Stock Prices page for your future reference.
© PandaCash